Teorema de Pitágoras

 

Hace años, un hombre llamado Pitágoras descubrió un hecho asombroso sobre triángulos:

 

Si el triángulo tiene un ángulo recto (90°)...

... y pones un cuadrado sobre cada uno de sus lados, entonces...

... ¡el cuadrado más grande tiene exactamente la misma área que los otros dos cuadrados juntos!

El lado más largo del triángulo se llama "hipotenusa", así que la definición formal es:

En un triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los otros dos lados (llamamos "triángulo rectángulo" a un triángulo con un ángulo recto)

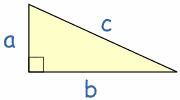Entonces, el cuadrado de a (a²) más el cuadrado de b (b²) es igual al cuadrado de c (c²): a2 + b2 = c2

¿Seguro... ?

Veamos si funciona con un ejemplo. Un triángulo de lados "3,4,5" tiene un ángulo recto, así que la fórmula debería funcionar.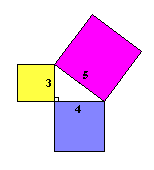

Veamos si las áreas son la misma: 32 + 42 = 52 Calculando obtenemos: 9 + 16 = 25 ¡sí, funciona!

¿Por qué es útil esto?

Si sabemos las longitudes de dos lados de un triángulo con un ángulo recto, el Teorema de Pitágoras nos ayuda a encontrar la longitud del tercer lado. (¡Pero recuerda que sólo funciona en triángulos rectángulos!)

¿Cómo lo uso?

Escríbelo como una ecuación:

a2 + b2 = c2

Ahora puedes usar álgebra para encontrar el valor que falta, como en estos ejemplos:

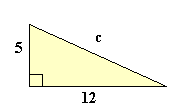
a2 + b2 = c2 52 + 122 = c2 25 + 144 = 169 c2 = 169 c = √169 c = 13

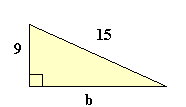
a2 + b2 = c2 92 + b2 = 152 81 + b2 = 225 Resta 81 a ambos lados b2 = 144 b = √144 b = 12

¡Y Puedes Demostrarlo Tú Mismo!

Consigue papel y tijeras, y usa la siguiente animación como guía:
	Dibuja un triángulo rectángulo en el papel, dejando mucho espacio alrededor. Dibuja un cuadrado sobre la hipotenusa (el lado más largo) Dibuja un cuadrado del mismo tamaño en el otro lado de la hipotenusa Dibuja líneas como en la animación, así: Recorta los trozos Colócalos de manera que puedas demostrar que el cuadrado grande tiene la misma área que los cuadrados en los otros lados juntos

Otra Demostración, Muy Simple

Aquí tienes una de las demostraciones más antiguas de que el cuadrado grande tiene la misma área que los otros cuadrados juntos.
	Mira la animación, y presta atención cuando se empiecen a mover los triángulos. Quizás quieras verla varias veces para entender bien lo que pasa. El triángulo violeta es el importante.

También tenemos una demostración sumando las áreas.

Aplicaciones del teorema de Pitágoras:

1 Conociendo los dos catetos calcular la hipotenusa

     

Ejemplo: Los catetos de un triángulo rectángulo miden en 3 m y 4 m respectivamente. ¿Cuánto mide la hipotenusa?

2 Conociendo la hipotenusa y un cateto, calcular el otro cateto

     

Ejemplo: La hipotenusa de un triángulo rectángulo mide 5 m y uno de sus catetos 3 m. ¿Cuánto mide otro cateto?

3 Conociendo sus lados, averiguar si es rectángulo

Para que sea rectángulo el cuadrado de lado mayor ha de ser igual a la suma de los cuadrados de los dos menores.
Ejemplo: Determinar si el triángulo es rectángulo.