Super Barbie real makeover

Super Barbie real makeover | juegos gratis con Games68.com

Rapunzel hospital recovery

Rapunzel hospital recovery | juegos gratis con Games68.com

Angry Birds

Angry Birds para Blogger

MARÍA DEL REFUGIO AGUILAR Y TORRES

 

El 21 de Septiembre de 2015 se abrirá el año jubilar de conmemoración del natalicio de nuestra Venerada Madre Fundadora María del Refugio Aguilar y Torres, cuyo aiversario celebrativo será el 21 de septiembre de 2016.
El día jueves 16 de julio, en la tarde, el Santo Padre Francisco recibió en audiencia al prefecto de la Congregación de las Causas de los Santos, cardenal Angelo Amato, durante la cual el Santo Padre autorizó la promulgación de los decretos de virtudes heroicas de ocho siervos de Dios.

Con gran alegría le participo que entre los nuevos venerables se encuentra María del Refugio Aguilar, culminando con esto una etapa muy importante en la causa de canonización de la fundadora de las Hermanas Mercedarias del Santísimo Sacramento. Llama la atención que a tan sólo quince días de la Consulta de cardenales el Santo Padre firmara la promulgación del decreto, sobre todo porque el texto del mismo nos fue entregado en italiano para que nosotros lo tradujéramos al latín (versión que se publicará en las Actas de la Congregación de las Causas de los Santos), traducción que hicimos llegar a dicha Congregación ¡el mismo jueves 16 de julio en la mañana!



Es significativo que la promulgación tuviera lugar el día que la Iglesia celebra a la Virgen del Carmen, de quien María del Refugio era muy devota; estando por iniciar la Asamblea congregacional; y a unas semanas de que inicie el año jubilar con motivo del 150 aniversario de su nacimiento.

El hecho de que a María del Refugio la podamos llamar en adelante “Venerable”, implica, entre otras cosas, que la Iglesia la reconoce como ejemplo de vida cristiana y que a sus restos los considera, desde el día de ayer, Reliquias. Sin embargo, debemos esperar la beatificación para rendir culto a la figura, por lo que deben evitarse manifestaciones de culto indebido, como sería colocar su fotografía o alguna reliquia en el presbiterio; representarla con aureola; darle el título de santa, etc.

Ahora los trabajos deberán enfocarse, principalmente, a profundizar en el conocimiento de la figura, la difusión y a pedir a Dios que por intercesión de ella nos conceda el milagro necesario para su beatificación.

Uno mi acción de gracias a la de Ustedes y, de mi parte, sinceras y fraternas felicitaciones a todas y cada una de las Hermanas Mercedarias del Santísimo Sacramento, augurando que este paso en la causa de canonización las anime a seguir correspondiendo a Dios con entusiasmo y alegría.ació en San Miguel de Allende (México) el 21 de septiembre

 

Razonamiento Logico Matematico

Definición de razonamiento lógico

Cuando una persona razona, desarrolla un razonamiento. Razonar es la actividad mental que permite lograr la estructuración y la organización de las ideas para llegar a una conclusión.
La lógica, por su parte, es la ciencia dedicada a la exposición de las formas, los métodos y los principios del conocimiento científico. Algo lógico, en este sentido, es aquello que respeta estas reglas y cuyas consecuencias resultan justificadas, válidas o naturales.
Un razonamiento lógico, en definitiva, es un proceso mental que implica la aplicación de la lógica. A partir de esta clase de razonamiento, se puede partir de una o de varias premisas para arribar a una conclusión que puede determinarse como verdadera, falsa o posible.

El razonamiento lógico se puede iniciar a partir de una observación (es decir, una experiencia) o de una hipótesis. El proceso mental de análisis puede desarrollarse de distintas maneras y convertirse en un razonamiento inductivo, un razonamiento deductivo, etc. Según la clase de razonamiento empleada, la conclusión tendrá mayor o menor posibilidad de resultar válida. La conclusión encuentra su base en las premisas iniciales: el razonamiento lógico es el camino que vincula ambas partes. El resultado del razonamiento tendrá un cierto grado de probabilidad en cuanto a su veracidad, siempre que los razonamientos lógicos sean válidos.
Supongamos que una mujer visita un país que no conoce. La primera persona con quien entabla conversación, habla en italiano. Lo mismo ocurre con la segunda y la tercera. A partir de un razonamiento lógico, puede inducir que todas las personas en ese país hablan italiano.
Hay muchas personas, fundamentalmente menores, que aún no han conseguido hacer un uso correcto del razonamiento lógico o que directamente necesitan mejorar al respecto. ¿Cómo pueden conseguir ese objetivo? Llevando a cabo la utilización de una serie de recursos, como juegos.
En concreto, en estos momentos, gracias al uso constante que hacemos de teléfonos móviles y tabletas, han surgido distintas aplicaciones que ayudan en ese aspecto. Así, las hay que logran desarrollar el razonamiento lógico mediante entretenimientos como sudokus hasta las que apuestan por los puzzles, sin olvidar las apps que hacen lo propio basándose en ejercicios habituales que están presentes en las pruebas de inteligencia.
Hay muchos niños que, además, tienen dificultades a la hora de poder hacer uso del razonamiento lógico para resolver problemas matemáticos de distinta complejidad. De ahí que sus padres y profesores deban ayudarles explicándoles a la perfección y de manera sencilla los distintos conceptos matemáticos que están utilizando e incluso recurriendo a pizarras, programas interactivos para ordenadores o esquemas sencillos que les permitan ir conociendo todos los pasos que hay que dar para llegar a una solución final y absolutamente certera.
Dentro del ámbito universitario, no podemos olvidar que existen diversas carreras que desarrollan su programación en base al razonamiento lógico o que este es uno de sus pilares fundamentales. Nos estamos refiriendo a grados tales como Matemáticas, Estadística Aplicada, Ingeniería de Tecnología de Minas y Energía, Física, Derecho, Ingeniería Informática, Filosofía, Física o Fisioterapia, entre otras muchas más.

 

EJERCICIOS PARA RESOLVER DE RAZONAMIENTO LOGICO MATEMATICO. 

A continuación proponemos ejercicios para que puedas practicar, sólo necesitas tener conocimientos básicos de matemática para resolverlos, te recomiendo que antes de ver la solución trates de resolverlos por todos los medios y sólo en caso que no puedas hacerlo veas la solución. Suerte!

Ejercicio 1

Se tiene 12 barras de chocolate, de las cuales 4 están enumeradas con el número 6; 4 con el número  5 y 4 con el número 1. Se distribuye las 12 barras en tres bolsas, A, B y C con igual número de barras. Si la suma de los números de la bolsa A es igual a 19, la de B es igual a 17 y la de C es igual a 12,  entonces es cierto que la bolsa C tiene: (ver solución)
A) Tres barras con el número 1.                   B) Dos barras con el número 6.
C) Dos barras con el número 1.                   D) Ninguna barra con el número 5.
E) Una barra con el número 6.
 
Ejercicio 2
De cinco futbolistas, donde ninguno tiene la misma cantidad de goles convertidos, se sabe que Claudio tiene dos goles más que Abel, Flavio tiene dos goles más que Roberto, pero uno menos que Abel y Ándres más goles que Roberto, pero menos que Abel. ¿Cuántos goles menos que Claudio tiene Ándres? (ver solución)
A) 1         B) 3          C) 5         D) 2         E) 4

Ejercicio 3
En una caja, se tiene 200 canicas de color verde, 200 de color rojo, 200 de color azul, 200 de color  negro y 250 de color amarillo. ¿Cuál es el  menor número de canicas que se debe extraer al azar para  tener, con certeza, al menos 100 canicas del mismo color? (ver solución)
A) 497       B) 498      C) 495      D) 496      E) 494

Ejercicio 4
Se tiene tres ciudades M, N y P. Un empresario que viaja en avión, cuando va de M hacia N tiene que atrasar su reloj 2 horas al llegar a N y cuando va de M hacia P debe adelantarlo 3 horas al llegar a P. Si sale de P hacia N, a las 11 p.m. y el viaje dura 4 horas, ¿qué hora es en N cuando llega? (ver solución)
A) 11 p.m.     B)  7 p.m.     C)  8 p.m.       D) 10 p.m.      E)  9 p.m.

Ejercicio 5
Una receta exige 4 litros de agua: si tuvieras una jarra de 4 litros no habría problema pero no posees más  que 2 jarras sin graduar, una de 5 litros y otra de 3. ¿Es posible medir los 4 litros que  necesitamos?
(ver solución)
A) No es posible
B) Es posible
C) Solo en forma aproximada
D) No se puede responder
E) Pregunta mal formulada

Ejercicio 6
En la avenida I hay cinco casas (1, 2, 3, 4, 5) que están en línea recta. Cuatro encuestadores (P, Q, R, T)  deben visitar, cada uno, solo una de las cinco casas.
Analice la siguiente información:
- Los encuestadores P y Q estuvieron separados por una casa.
- Los encuestadores R y T estuvieron separados por dos casas.
- La misma casa no pudo haber sido visitada simultáneamente por dos encuestadores.
De acuerdo con la información dada ¿Cuáles casas no pudieron ser visitadas? (ver solución)

A) La 1 y la 3        B) La 2 y la 4          C) La 2 y la 5
D) La 3 y la 4        E) La 3 y la 5

Ejercicio 7

Se le pregunta la hora a un señor y este contesta: "Dentro de 20 minutos mi reloj marcará las 10 y 32". Si el reloj está adelantado de la hora real 5 minutos, ¿qué hora fue hace 10 minutos exactamente?
(ver solución)

A) 10:10 min        B) 10:07 min         C) 10:12 min
D) 09:50 min        E) 09:57min


Ejercicio 8
En una de las tres cajas hay un tesoro, la única ayuda que dispone el adivinador es saber que uno y sólo uno de los letreros está mal. ¿Dónde está el tesoro? (ver solución)
A) En II            B) En III           C) En I o II
D) En I             E) En I o III


Ejercicio 9
Juan es el doble de rápido que Ángel y este dos veces más rápido que Omar. Para realizar una obra trabajaron durante 3 horas al término de las cuales se retira Omary los otros culminan la Obra en 5 horas más de trabajo. ¿Cuántas horas emplearía Omar en realizar 1/3 de la Obra? (ver solución)
A) 30       B) 10     C) 20        D) 15      E) 25


Ejercicio 10
Se compran tres manzanas por $10 y se venden cinco manzanas por $20, ¿Cuántas manzanas se deben vender para ganar $150? (ver solución)
A) 125      B) 225       C) 300       D) 150       E) 100


Ejercicio 11
Lucía fue al médico, éste le recetó tomar 4 pastillas, una pastilla cada 6 horas, ¿En qué tiempo podrá terminar de tomar todas las pastillas? (ver solución)

A) 28 horas

B) 24 horas

C) 20 horas

D) 18 horas

E) 32 horas

Ejercicio 12
Si dos estudiantes pueden resolver 2 preguntas en 2 minutos, ¿Cuántos estudiantes se necesitarán para resolver 4 preguntas en 4 minutos? (ver solución)

A) 4

B) 8

C) 16

D) 2

E) 6

Ejercicio 13
En cierto examen Rosa obtuvo menos puntos que María, Laura menos puntos que Lucía, Noemí el mismo puntaje que Sara;  Rosa más que Sofía; Laura el mismo puntaje que María y Noemí más que Lucía. ¿Quién obtuvo menos puntaje? (ver solución)

A) Laura

B) María

C) Rosa

D) Sofía

E) Sara

Ejercicio 14
En una ferretería tienen un stock de 84m de alambre, y diario cortan 7m. ¿En cuántos días habrán cortado todo el alambre? (ver solución)

A) 13

B) 12

C) 11

D) 10

E) 9

Ejercicio 15
En  una  habitación  hay  11  pelotas  amarillas,  13  azules  y  17 verdes. Si se le pide a un ciego sacar las pelotas, ¿cuál es el mínimo número de pelotas que debe extraer para que obtenga con total seguridad 11 pelotas del mismo color? (ver solución)

A) 24

B) 11

C) 28

D) 31

E) 30

Ejercicio 16
En una caja grande hay 6 cajas dentro de cada una de estas cajas hay 3 cajas, dentro de estas hay 2  cajas. ¿Cuántas cajas hay en total? (ver solución)

A) 36

B) 18

C) 51

D) 61

E) N.A.

Ejercicio 17
Cinco pueblos A, B, C, D y E (no necesariamente en ese orden) se encuentran a lo largo de una carretera. Las distancias (en kilómetros) entre ellos se muestran en el siguiente cuadro:
     A B  C D E
A  0 3  3  1  6
B  3 0  6  2  3
C  3 6  0  4  9
D  1 2  4  0  5
E  6 3  9  5  0
El orden correcto de estos pueblos a lo largo de la carretera es: (ver solución)

A) A C D B E	B)  C A D B E	C)  C D A B E
D) C B D A E	E) A B C D E

Ejercicio 18
Andrea, Braulio, Carlos, Dante y Esteban están sentados formando una ronda, en el orden indicado. Andrea dice el numero 53, Braulio el 52, Carlos el 51, Dante el 50, y así sucesivamente. ¿Quién dice el numero 1? (ver solución)

A) Andrea

B) Carlos

C) Braulio

D) Esteban

E) Dante

Ejercicio 19
Diana nació dos años antes que Pedro y Ramiro tres años antes que Andrés. Si Pedro es el hermano mayor de Esteban y Andrés y, además, Esteban nació tres años después que Andrés, ¿Cuál de los cinco es el menor? (ver solución)

A) Diana

B) Pedro

C) Ramiro

D) Esteban

E) Andrés

Ejercicio 20
Un sapo se dirige dando saltos desde el punto A hacia el punto B, distantes entre sí 100 cm. Si entre ambos puntos está el punto C a 12.5 cm de B, ¿con cuántos saltos llegará a C, si en cada salto avanza la mitad de la distancia que le falta para llegar a B? (ver solución)

A) 4

B) 3

C) 6

D) 5

E) 2

Ejercicio 21
Luz, Ruth, Katty y Nora tienen profesiones diferentes y viven en las ciudades A, B, C y D. Una de ellas es profesora, Nora es enfermera, la que es contadora vive en A y la bióloga nunca ha emigrado de C. Luz vive en D y Katty no vive ni en A ni en B. ¿Qué profesión tiene Luz y dónde vive Katty? (ver solución)
A) Luz es bióloga y Katty vive en C.
B) Luz es profesora y Katty vive en D.
C) Luz es profesora y Katty vive en C.
D) Luz es contadora y Katty vive en D.
E) Luz es enfermera y Katty vive en C.

Ejercicio 22
Si una ficha roja equivale a 3 azules y cada azul equivale a 2 blancas, ¿a cuánto equivaldrán 120 blancas? (ver solución)

a) 20 rojas

b) 20 azules

c) 15 azules

d) 10 rojas

e) NA

Ejercicio 23
Si en el  producto  indicado  27x36, cada factor aumenta  en  4  unidades; ¿Cuánto aumenta el producto original? (ver solución)

A) 320

B) 288

C) 328

D) 268

E) 220

Ejercicio 24
Un turista alquila un auto a $30 diarios y adicionalmente abona $ 0,1 por km recorrido. El auto le rinde 35 km por galón en la ciudad y 50 km por galón en carretera, a un costo de $3,5 por galón. Si en una semana lo que recorre en carretera es 5 veces lo recorrido en ciudad, calcule el costo total en  dólares, del alquiler del auto en dicha semana al cabo de la cual se recorrió 600 km en total. (ver solución)

A. 315

B. 350

C. 425

D. 450

Ejercicio 25

De Carla, Betty y Jessica se sabe que solo una de ellas miente, y que la que miente es la menor de las tres. Si Betty dice que Carla y Jessica son mentirosas, se puede afirmar que: (ver solución) (1)
A) Betty es mayor que Carla
B) Carla y Betty son mayores que Jessica
C) Carla y Jessica son mayores que Betty
D) Jessica y Betty  son mayores que Carla
E) Betty es mayor que Jessica

Ejercicio 26
Paco llena un vaso con vino y bebe una cuarta parte del contenido; vuelve a llenarlo, esta vez con agua, y bebe una tercera parte de la mezcla; finalmente, lo llena nuevamente con agua y bebe la mitad del contenido del vaso. Si la capacidad del vaso es de 200mL, ¿qué cantidad de vino queda finalmente en el vaso? (ver solución)

A) 100 mL

B) 40 mL

C) 60 mL

D) 80 mL

E) 50 mL

Ejercicio 27

Cuatro amigas de Carola, cada una con lentes oscuros, tienen la siguiente conversación:
Betty: Yo no tengo ojos azules
Elisa: Yo no tengo ojos pardos
María: Yo tengo ojos pardos
Leyla: Yo no tengo ojos negros
Si se sabe que solo una tiene ojos azules y las demás tienen ojos pardos, y que solo una de las cuatro amigas miente, ¿Quién tiene ojos azules? (ver solución)

A) Betty

B) María

C) Elisa

D) Leyla

E) Carola

Ejercicio 28

Roberto es el único hijo del abuelo de Javier, y Rosario es la única nuera del abuelo de Roberto. Si el hijo único de Javier tiene cinco años y de una generación a otra consecutiva transcurren 20 años, ¿cuál es la suma de las edades del abuelo y bisabuelo de Javier? (ver solución)

A) 135 años

B) 140 años

C) 155 años

D) 150 años

E) 145 años

Ejercicio 29

María califica 25 exámenes por hora y Rosa 20 exámenes por hora. Cada una tiene que calificar 500 exámenes. Si María terminó de calificar. ¿Cuántos exámenes le faltan por calificar a Rosa? (ver solución)

A) 100

B) 60

C) 90

D) 120

E) 50

Ejercicio 30

Un niño tiene el mismo número de hermanas que de hermanos, y una de sus hermanas tiene la mitad de hermanas que de hermanos. ¿Cuántos niños hay en la familia? ¿Cuántos son hombres y cuántas mujeres? (ver solución)
A) 5, 3 hombres y 2 mujeres
B) 4, 2 hombres y 2 mujeres
C) 5, 2 hombres y 3 mujeres
D) 7, 4 hombres y 3 mujeres

Ejercicio 31

Inés y Juan hicieron un extraño acuerdo. Inés miente los Miércoles, Jueves y Viernes, pero dice la verdad el resto de la semana. Juan miente los Domingos, Lunes y Martes, pero dice la verdad en todos los otros días. Cierto día ambos dijeron: "Mañana es día de mentir", ¿en que día dijeron esto? (ver solución)

A) Lunes

B) Martes

C) Miércoles

D) Viernes

E) Sábado

Ejercicio 32

¿Cuántos árboles hay en un campo triangular que tiene 10 árboles en cada lado y un árbol en cada esquina? (ver solución)

(A) 30

(B) 33

(C) 29

(D) 27

(E) 10

Ejercicio 33

Se desea colocar postes igualmente espaciados en el perímetro de un terreno rectangular de 280 m de largo por 120 m de ancho. Si se sabe que debe colocarse un poste en cada esquina y el número de postes debe ser el menor posible, determínese el número total de postes por colocar. (ver solución)

A) 24

B) 20

C) 48

D) 40

E) 18

Ejercicio 34

Con tres frutas diferentes: papaya, pera y piña. ¿Cuántos sabores diferentes de jugo se podrá preparar con estas frutas? (ver solución)

A) 7

B) 10

C) 19

D) 24

E) 21

Ejercicio 35
La Empresa Eléctrica va instalar postes equidistantes cada 5m a lo largo de un pasaje de 95m de tal forma que haya uno al inicio y otro al final. Además emplean 15 minutos para colocar cada poste. ¿Cuánto tiempo demorarán en colocar todos los postes? (ver solución)

A. 4 horas 45 minutos

B. 2 horas 30 minutos

C. 6 horas

D. 5 horas

E.  3 horas

Ejercicio 36
Se tiene una colección de 7 tomos de libros de 700 páginas cada uno. Si cada tapa tiene un espesor de 0.25cm, y las hojas por cada tomo, un espesor de 4cm, ¿Cuánto recorrerá una polilla que se encuentra en la primera página del primer tomo a la última página del último tomo? (ver solución)

A) 22 cm

B) 31 cm

C) 20 cm

D) 19 cm

E) 21cm

Problemas de Razonamiento Lógico resueltos.

Problema 01

Un señor tiene cien mil cabellos. Si cada tres días pierde 360 cabellos y cada semana le crecen 140, ¿en cuántos días se quedará completamente calvo?
A) 1000          B) 820            C) 960           D) 780       E) 980

Problema 02

De un grupo de 60 estudiantes la treceava parte de los varones son gorditos. si se sabe que los varones son mayoría, ¿cuántos gorditos hay en el grupo, sabiendo que hay más de 10 mujeres?

A) 3

B) 6

C) 4

D) 13

E) 5

Problema 03

Seis amigos se sientan alrededor de una caja de cerveza. Jaime no está sentado al lado de Willy ni de  Héber. César no está sentado al lado de Rubén ni de Héber. Willy no está al lado de Rubén ni de César.  Manuel está junto a Willy, a su derecha. ¿Quién está sentado a la derecha de César?

A) Jaime                 B) Manuel                     C) Willy                    D) Rubén              E) Héber

Problema 04

Para llegar a su colegio, un alumno debe dar 560 pasos, ¿Cuántos minutos demorará en llegar, si da dos pasos en la cuarta parte de  medio minuto?  (ver solución)

Problema 05

En la sucesión mostrada de figuras construidas con palitos de fósforo, halle el doble del número de palitos de la figura que ocupa el decimotercer lugar. (ver solución)

A) 448

B) 336

C) 194

D) 390

E) 364

Problema 06

Carlos estudia matemáticas cada 2 días, lenguaje cada 4 días e ingles cada 3 días, pero hoy que es viernes, estudia los tres cursos. Determine qué día de la semana volverá a estudiar los tres cursos, si es lo más pronto posible. (ver solución)

A) Lunes

B) Martes

C) Miércoles

D) Jueves

E) Viernes

Problema 07

Ana, Bertha, Carla y Diana tienen juntas 200 monedas de oro y juegan con su dinero de la siguiente manera: Ana le da la mitad que tiene a Bertha, y luego Bertha le da la mitad de lo que tiene a Carla y en seguida Carla le da la mitad de lo que tiene a Diana, quien finalmente le da 10 monedas a Ana. Si al final del juego todas tienen igual cantidad de dinero, ¿cuántas monedas tenía Ana al comenzar el juego? (ver solución)

A) 10

B) 40

C) 50

D) 60

E) 80

Problema 08

Rodrigo compra 60 CD a $40.0 y vende 40 CD a $60.0. ¿Cuántos CD tendrá que vender para ganar $1200? (ver solución)

A) 1440

B) 1200

C) 1500

D) 1450

E) 1800

Problema 09

Tres conejos cuestan como 8 gallinas, 16 gallinas valen lo mismo que 15 cuyes. Si se sabe que 5 cuyes cuestan 20 soles. ¿Cuánto cuestan 10 conejos? (ver solución)

A) $ 100

B) $ 60

C) $ 70

D) $ 40

E) $ 50

Problema 10

En un torneo de ajedrez, tres amigos jugaron entre si todos contra todos. Si se jugaron 21 partidas en total y  todos jugaron el mismo numero de partidas. ¿Cuántas partidas jugó cada uno? (ver solución)

Problema 11

A una vara le realizamos 7 cortes y a cada parte obtenida le realizamos 8 cortes. ¿En cuántas partes en total ha sido dividida la vara? (ver solución)

A) 7

B) 8

C) 56

D) 72

E) 63

Problema 12

Si Violeta sube la escalera de su casa de 3 en 3, da 8 pasos más que subiendo de 5 en 5. Si sube la escalera de su trabajo de 4 en 4, da 6 pasos más que subiendo de 6 en 6. ¿Cuál es la diferencia de peldaños entre ambas escaleras? (ver solución)

Problema 13
Una hormiga debe subir 95 escalones, pero cada hora, por cada 5 escalones que sube baja 2. ¿Cuantas horas tardará en subir los 95 escalones? (ver solución)

Problema 14

¿Cuál es el mayor número natural, formado por dígitos distintos, tal que al multiplicar sus dígitos se obtiene como resultado 40? (ver solución)

Problema 15

Por cada nueve panes que compró María, le regalaron un pan. Si recibió 770 panes en total, ¿Cuántos panes le regalaron? (ver solución)

A) 77

B) 74

C) 71

D) 88

E) 66

Problema 16

A un alumno se le pregunta que día es hoy y contesta: "Te mentiría si te digo que hoy no es Jueves". Si éste alumno está diciendo la verdad, ¿en qué día de la semana se le hizo la pregunta? (ver solución)

A) Jueves

B) Miercoles

C) Martes

D) No se sabe

E) Domingo

Problema 17

Si por $10 me dieran 4 chocolates más de los que recibo normalmente, cada uno resultaría costando $1, indique cuántos chocolates recibo normalmente por $5. (ver solución)

A) 2

B) 3

C) 4

D) 5

E) 6

Logica y Conjuntos

Teoría de Conjuntos

 

NOCION INTUITIVA DE CONJUNTO

Un conjunto es la reunión en un todo de objetos bien definidos y diferenciables entre si, que se llaman elementos del mismo. Si a es un elemento del conjunto A se denota con la relación de pertenencia a Î A.
En caso contrario, si a no es un elemento de A se denota aÏ A.
 
Ejemplos de conjuntos:

• Æ : el conjunto vacío, que carece de elementos.
• N: el conjunto de los números naturales.
• Z: el conjunto de los números enteros.
• Q : el conjunto de los números racionales.
• R: el conjunto de los números reales.
• C: el conjunto de los números complejos.

 
Se puede definir un conjunto:

• por extensión, enumerando todos y cada uno de sus elementos.
• por comprensión, diciendo cuál es la propiedad que los caracteriza.

 
Un conjunto se suele denotar encerrando entre llaves a sus elementos, si se define por extensión,
o su propiedad característica, si se define por comprensión. Por ejemplo:

• A := {1,2,3, ... ,n}
• B := {pÎ Z | p es par}

 
Se dice que A está contenido en B (también que A es un subconjunto de B o que A es una parte de B),
y se denota A Í B, si todo elemento de A lo es también de B, es decir, a Î A Þ a Î B. Dos conjuntos A y B se dicen iguales, y se denota A = B, si simultáneamente A Í B y B Í A;
esto equivale a decir que tienen los mismos elementos (o también la misma propiedad característica).
Para cualquier conjunto A se verifica que ÆÍ A y A Í A;
B Í A es un subconjunto propio de A si A ¹ Æ y B ¹ A.
El conjunto formado por todos los subconjuntos de uno dado A se llama partes de A, y se denota à (A).
Entonces, la relación B Í A es equivalente a decir B Î Ã (A). Ejemplos:
 
Si A = {a,b} entonces à (A) = {Æ ,{a},{b},A}. Si a Î A entonces {a} Îà (A).
Cuando en determinado contexto se consideran siempre conjuntos que son partes de uno dado U,
se suele considerar a dicho U como conjunto universal o de referencia.

OPERACIONES ENTRE CONJUNTOS

Dados dos conjuntos A y B, se llama diferencia al conjunto A - B := {a Î A | a Ï B}.
Asimismo, se llama diferencia simétrica entre A y B al conjunto A D B := (A - B) È (B - A). Si A Î Ã (U), a la diferencia U - A se le llama complementario de A respecto de U,
y se denota abreviadamente por A' (U se supone fijado de antemano).
Es fácil ver que si A y B son subconjuntos cualesquiera de U se verifica:

• Æ ' = U .
• U ' = Æ .
• (A')' = A .
• A Í B Û B' Í A' .
• Si A = { x Î U | p(x) es una proposición verdadera} entonces A' = { x Î U | p(x) es una proposición falsa}.

 
Se llama unión de dos conjuntos A y B al conjunto formado por objetos que son elementos de A o de B,
es decir: A È B := { x | x Î A Ú x Î B}. Se llama intersección de dos conjuntos A y B al conjunto formado por objetos que son elementos de A y de B,
es decir: A Ç B := {x | x Î A Ù x Î B}.
Si A y B son subconjuntos de un cierto conjunto universal U, entonces es fácil ver que A - B = A Ç B'.
En este caso, la llamadas operaciones booleanas (unión e intersección) verifican las siguientes propiedades :

PROPIEDADES	UNION	INTERSECCION
1.- Idempotencia	A È A = A	A Ç A = A
2.- Conmutativa	A È B = B È A	A Ç B = B Ç A
3.- Asociativa	A È ( B È C ) = ( A È B ) È C	A Ç ( B Ç C ) = ( A Ç B ) Ç C
4.- Absorción	A È ( A Ç B ) = A	A Ç ( A È B ) = A
5.- Distributiva	A È ( B Ç C ) = ( A È B ) Ç ( A È C )	A Ç ( B È C ) = ( A Ç B ) È ( A Ç C )
6.- Complementariedad	A È A' = U	A Ç A' = Æ

 
Estas propiedades hacen que partes de U con las operaciones unión e intersección tenga una estructura de álgebra de Boole.
Además de éstas, se verifican también las siguientes propiedades:

• A È Æ = A , A Ç Æ = Æ ( elemento nulo ).
• A È U = U , A Ç U = A ( elemento universal ).
• ( A È B )' = A' Ç B' , ( A Ç B )' = A' È B' ( leyes de Morgan ).

 
Dados dos conjuntos A y B, se define el producto cartesiano de ambos como el conjunto de pares ordenados:
  A ´ B := { (a,b) : a Î A Ù b Î B}
Dos pares (a,b) y (c,d) de A ´ B son iguales si a = c y b = d; análogamente, dados cuatro conjuntos A,B,C,D se verifica
 
A ´ B = C ´ D Û ( A = C Ù B = D )
Se llama grafo relativo a A ´ B a todo subconjunto G Í A ´ B.
Dado un grafo G relativo a A ´ B, se llama proyección de G sobre A al conjunto
 
Proy_AG := { a Î A : (a,b) Î G, $ b Î B}
Análogamente se define la proyección Proy_BG de G sobre B.
Por último, los conceptos anteriores pueden generalizarse a familias de conjuntos.
Si para cada elemento i de un conjunto (de índices ) I se tiene un conjunto A_i , entonces se define el conjunto { A_i : i Î I }
y se denomina familia de conjuntos indicada por I. También se suele denotar por { A_i } _{i Î I} .
De forma análoga se define una familia de elementos ( a_i ) _{i Î I} .
Dada una familia de conjuntos { A_i } _{i Î I} se definen:
 

• È _{i ÎI} A_i := { a : a Î A_i , $ i Î I }
• Ç _{i Î I} A_i := { a : a Î A_i , " i Î I }
• Õ _{i Î I} A_i := { (a_i) : a_i Î A_i , " i Î I }

 
Las propiedades de la unión e intersección siguen siendo válidas para familias de conjuntos, y en particular las leyes de Morgan :
  ( È _{i Î I} A_i )' = Ç _{i Î I} A'_i     ,    (Ç_{i Î I} A_i )' = È_{i Î I} A'_i DIAGRAMAS DE VENN Los conjuntos de suelen representar gráficamente mediante "diagramas de Venn", con una línea que encierra a sus elementos.
Así, todas las operaciones entre conjuntos se pueden representar gráficamente con el fin de obtener una idea más intuitiva.
A Í B

 
A È B

 
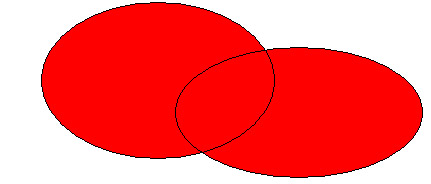
A Ç B

 
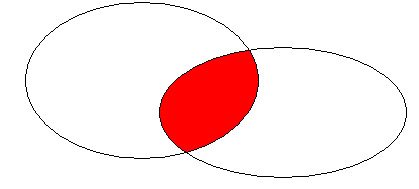
A - B

 
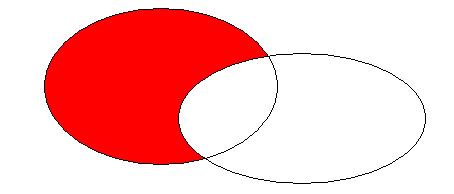
A D B

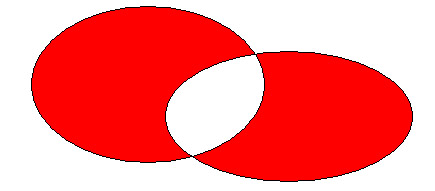
RELACION ENTRE LA TEORIA DE CONJUNTOS Y LA LOGICA PROPOSICIONAL

Existe una relación muy estrecha entre la Teoría de Conjuntos y la Lógica Proposicional.
Para mostrar dicha relación, denotemos por letras mayúsculas A,B ... los conjuntos y
por las correspondientes minúsculas a,b ... sus propiedades características
(es decir, la proposición lógica que caracteriza a los elementos de cada conjunto);
entonces se tiene la siguiente correspondencia:
 
 

conjuntos	A Í B	A = B	A È B	A Ç B	A'	A - B	A D B
proposiciones	a Þ b	a Û b	a Ú b	a Ù b	a'	a Ù b'	a Ú b

Además, el conjunto vacío se corresponde con una contradicción y el conjunto universal con una tautología.
Mediante esta correspondencia, todos los resultados sobre conjuntos se pueden reescribir en términos de lógica
proposicional y viceversa; a modo de ejemplo:
 
 

A È ( A Ç B ) = A	a Ú ( b Ù c ) Û a
A È ( B Ç C ) = ( A È B ) Ç ( A È C )	a Ú ( b Ù c ) Û ( a Ú b ) Ù ( a Ú c )
( A È B )' = A' Ç B'	( a Ú b )' Û a' Ù b'

PROPOSICIONES CON CUANTIFICADORES
Los símbolos " (cuantificador universal) y $ (cuantificador existencial) se utilizan en Matemáticas para
enunciar proposiciones logicas relativas a objetos matemáticos.
Sea A un conjunto y p(x) una proposición o propiedad que hace referencia a un elemento x.
(1) Cuantificador universal : La expresión
        " x Î A Þ p(x)
se lee "para todo x que pertenece a A se verifica p(x)", representa la proposición
        { x Î A : p(x) } = A
(2) Cuantificador existencial : La expresión
        $ x Î A | p(x)
se lee "existe x que pertenece a A tal que p(x)", representa la proposición
        { x Î A : p(x) } ¹ Æ
 
La negación de cualquiera de las dos proposiciones anteriores se realiza negando la proposición p(x)
y cambiando el cuantificador universal por el cuantificador existencial, o viceversa.
Así, la negación de la proposición "" x Î A Þ p(x)" es "$ x Î A | p(x)' ", mientras que
la negación de "$ x Î A | p(x)" es "" x Î A Þ p(x)' "
 
 

 

 

Conjuntos finitos : Combinatoria

La Combinatoria es la parte de las Matemáticas que se dedica al estudio de los conjuntos finitos.
Puesto que la propiedad principal de estos conjuntos es que se puede representar su número de elementos
mediante un número natural (llamado cardinal de dicho conjunto), la tarea básica de la Combinatoria es
precisamente el cálculo del cardinal de dichos conjuntos.
Para dicho cálculo se necesita definir los llamados números combinatorios:
 
        (1) Números factoriales: se define n! mediante la ley de recurrencia
                        n! = n · (n-1)!
                y la condición inicial 0! := 1. De forma iterativa, se tiene
                        n! = n · (n-1) · (n-2) · ... · 3 · 2 · 1
        n! es el número de permutaciones de n elementos, es decir, es el número total de formas de ordenar n elementos
        de todas las formas distintas posibles.
 
        (2) Coeficientes binomiales: se definen por la fórmula
                        
        El número "n sobre k" es el número de combinaciones de n elementos tomados de k en k, es decir,
        el número de subconjuntos distintos de k elementos que tiene un conjunto con n elementos.
        Los coeficientes binomiales tienen dos propiedades básicas:
                (a)
                        
                (b)
                        
 
        Como aplicación de los números combinatorios y del Binomio de Newton, podemos contar el número total de
        subconjuntos que tiene un conjunto A con n elementos, es decir, el cardinal de partes de A; para ello, notemos
        que el número de tales subconjuntos se obtiene sumando el número de subconjuntos de 0 elementos más los de
        1 elemento, más los de 2 elementos, y así hasta los de n elementos, es decir:
 
                        
 
        Pero esta cantidad corresponde a desarrollar mediante el binomio de Newton la expresión
                (1+1)ⁿ  = 2ⁿ
        Así pues se obtiene que # Ã (A) = 2ⁿ si # A = n.
 
 

Proposiciones Simples y Compuestas

CONCEPTO DE PROPOSICIÓN

Es una oración aseverativa de la que tiene sentido decir que es verdadera o falsa.

• Expresión verbal que afirma o niega algo.

• Secuencia finita de signos con significado y sentido de ser calificado como verdadero o falso.

• Expresión lingüística susceptible de ser calificada de verdadera o falsa. hace referencia explicita a las oraciones aseverativas o enunciativas.

EJEMPLOS:
CIERTOS

• La raíz cuadrada de 4 es 2.
• Los bebes lloran.
• Un cuadrado tiene 4 lados.

FALSOS

• Todos los carros tiene 2 ruedas.
• 20 + 20 = 20.
• Ningún hombre sabe leer.

Proposiciones compuestas (Disyunción, Conjunción, Negación, Condicional, Bicondicional)

DISYUNCIÓN

La disyunción es un operador que opera sobre dos valores de verdad, típicamente los valores de verdad de dos proposiciones, devolviendo el valor de verdad verdadero cuando una de las proposiciones es verdadera, o cuando ambas lo son, y falso cuando ambas son falsas.

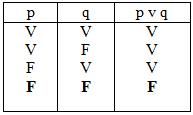
Tabla de verdad de la disyunción

p v q (se lee: ” p o q”)

EJEMPLOS:

p = ” El numero 2 es par”

q = ” la suma de 2 + 2 es 4″

entonces…

pvq: “El numero 2 es par o la suma de 2 + 2 es 4″

p = ” La raíz cuadrada del 4 es 2”

q = ” El numero 3 es par″

entonces…

pvq: “La raíz cuadrada del 4 es 2 o el numero 3 es par”

CONJUNCIÓN

La conjunción es un operador que opera sobre dos valores de verdad, típicamente los valores de verdad de dos proposiciones, devolviendo el valor de verdad verdadero cuando ambas proposiciones son verdaderas, y falso en cualquier otro caso. Es decir es verdadera cuando ambas son verdaderas.

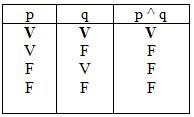
Tabla de verdad de la conjunción

 p ^ q (se lee: ” p y q”)

EJEMPLOS:

p = ” El numero 4 es par”

q = ”Siempre el residuo de los números pares es 2″

entonces…

p^q: “El numero 4 es par y Siempre el residuo de los números pares es 2″

p = ” El numero mas grande es el 34”

q = ”El triangulo tiene 3 lados″

entonces…

p^q: “El numero mas grande es el 34 y El triangulo tiene 3 lados”

NEGACIÓN

La negación es un operador que se ejecuta. sobre un único valor de verdad, devolviendo el valor contradictorio de la proposición considerada.

Tabla de verdad de Negación

EJEMPLOS

p:  “4 + 4 es igual a 9”

-p: “4 + 4 no es igual a 9″

p:  “El 4 es un numero par”

-p: “El 4 no es un numero par”

CONDICIONAL

El condicional material es un operador que opera sobre dos valores de verdad, típicamente los valores de verdad de dos proposiciones, devolviendo el valor de verdad falso sólo cuando la primera proposición es verdadera y la segunda falsa, yverdadero en cualquier otro caso.

La condicional de dos proposiciones p, q da lugar a la proposición; si p entonces q, se representa por p → q

Tabla de Verdad Condicional

EJEMPLOS

p:  “llueve”

q: “hay nubes”

p→q: “si llueve entonces hay nubes”

p:  “Hoy es miércoles”

q: “Mañana será jueves”

p→q: “Si Hoy es miércoles entonces Mañana será jueves”

BICONDICIONAL

El bicondicional o doble implicación es un operador que funciona sobre dos valores de verdad, típicamente los valores de verdad de dos proposiciones, devolviendo el valor de verdad verdadero cuando ambas proposiciones tienen el mismo valor de verdad, y falso cuando sus valores de verdad difieren.

Tabla de Verdad Bicondicional

EJEMPLOS

p:  “10 es un número impar”

q: “6 es un número primo”

p↔q: “10 es un número impar si y solo si 6 es un número primo”

p:  “3 + 2 = 7”

q: “4 + 4 = 8”

p↔q: “3 + 2 = 7  si y solo si 4 + 4 = 8″

Lógica matemática

Lógica matemática. Es la disciplina que trata de métodos de razonamiento. En un nivel elemental, la lógica proporciona reglas y técnicas para determinar si es o no valido un argumento dado. El razonamiento lógico se emplea en matemáticas para demostrar teoremas; en ciencias de la computación para verificar si son o no correctos los programas; en las ciencias física y naturales, para sacar conclusiones de experimentos; y en las ciencias sociales y en la vida cotidiana, para resolver una multitud de problemas. Ciertamente se usa en forma constante el razonamiento lógico para realizar cualquier actividad. 

 

La lógica estudia la forma del razonamiento, es una disciplina que por medio de reglas y técnicas determina si un argumento es válido. La lógica es ampliamente aplicada en la Filosofía, Matemáticas, Computación, Física. En la filosofía para determinar si un razonamiento es válido o no, ya que una frase puede tener diferentes interpretaciones, sin embargo la lógica permite saber el significado correcto. En las matemáticas para demostrar teoremas e inferir resultados matemáticas que puedan ser aplicados en investigaciones.
La evolución de la lógica está ligada a la evolución intelectual del ser humano, ya que como ciencia del razonamiento se puede afirmar que su historia representa la historia misma del hombre. La lógica surge desde el momento en que el hombre al enfrentarse a la naturaleza empieza a observar, experimentar, deduce y razona.
Durante el periodo 600 AC hasta 300 AC se desarrollaron en Grecia los principios formales de las matemáticas, a este periodo se le llamo periodo clásico en donde sus principales representantes son: Platón que el introdujo sus ideas y abstracciones; Aristóteles que presentó el razonamiento ductivo y sistemático y Euclides que fue el que tuvo mayor influencia ya que este estableció el método axiomático.

Platón

Platón, propone instaurar en Siracusa una utópica república dirigida por filósofos. Crea la Academia de Atenas que no era solo una institución filosófica, sino centro de formación política para jóvenes aristócratas. Según algunos especialistas, Platón edifica su teoría del conocimiento con el fin de justificar el poder emergente de la figura del filósofo. Sostiene la existencia de dos mundos -el mundo de las ideas y el de mundo físico de los objetos. Según Platón, lo concreto se percibe en función de lo abstracto y por tanto el mundo sensible existe gracias al mundo de las ideas. Platón escoge el formato diálogo como forma de transmisión del pensamiento.

Aristóteles

Los tratados de lógica de Aristóteles, conocidos como Organón, contienen el primer tratado sistemático de las leyes de pensamiento para la adquisición de conocimiento. Representan el primer intento serio que funda la lógica como ciencia.

Objetivos

El objetivo de la lógica matemática es cuestionar los conceptos y las reglas de deducción que son utilizadas en las matemáticas y esto constituye a la lógica una verdadera matemática.

Álgebra de la lógica

Parte de la lógica matemática basada en la aplicación de los métodos algebraicos al estudio de los objetos lógicos: clases y proposiciones. Por una parte, la proposición expresa un sentido (juicio); por otra, designa una verdad (V) o una mentira (M). Así, las proposiciones «El Volga desemboca en el mar Caspio» y «2 x 2= 4» expresan un sentido diferente, pero ambas designan una verdad (tienen el significado de V). 
El álgebra de la lógica examina las proposiciones sólo desde el punto de vista de su significado, con la particularidad de que se consideran equivalentes las que poseen un mismo significado de veracidad. 
El álgebra de la lógica utiliza la notación simbólica (Simbolismo lógico). Además de los símbolos de las proposiciones, se emplean símbolos para las operaciones: conjunción, disyunción, implicación, negación, con los cuales el álgebra de la lógica forma unas expresiones partiendo de otras. 
Una expresión será compuesta si ha sido formada por otras mediante operaciones algebraicas lógicas; en el caso contrario, será simple. Dos expresiones se llaman equivalentes si en cada combinación posible de significados de las expresiones simples en ellas contenidas presentan significados iguales. Así A ® B es equivalente a Aœ Ë B, dado que en las cuatro posibles combinaciones de significados de V y M para A y B: VV, VM, MV, MM, A ® B presenta el mismo significado que Aœ Ë B. 
En relación con los conceptos introducidos, se plantean en el álgebra de la lógica una serie de problemas a cuya resolución se aplica esta disciplina. Históricamente, el álgebra de la lógica surgió como álgebra de las clases (Boole) y sólo después fue interpretada como álgebra de las proposiciones. Con los trabajos de V. I. Shestakov y de Claude Shannon, el álgebra de la lógica encuentra amplia aplicación en la teoría de los esquemas eléctricos y de los esquemas con relés de contacto. 

HIPERBOLA

 La hipérbola es el lugar geométrico de los puntos de un plano cuya diferencia de distancias (d₁ y d₂) a dos puntos fijos llamados focos (F₁ y F₂) es constante.
El valor de esa constante es la distancia entre los vértices V₁ y V₂ de la hipérbola (2a).






La hipérbola también se puede definir como una cónica, siendo la intersección del cono y un plano cuyo ángulo es menor que el de su generatriz.

Elementos de la hipérbola

Los elementos de la hipérbola son:

• Focos: son los dos puntos fijos (F₁ y F₂).
• Radio vector: es la distancia R de un punto de la hipérbola (P) a cualquiera de los focos.
• Eje focal: es el eje de simetría E que une a los dos focos. También se llama eje transverso.
• Eje no transverso: es la mediatriz T del eje focal.
• Centro: es el punto medio O de los dos focos. También se puede definir como la intersección del eje focal y el transverso.
• Vértices: son los dos puntos de intersección del eje focal con la hipérbola (V₁ y V₂).

• Distancia focal: es la distancia 2c entre focos. También se denota como F₁F₂.
• Eje real: es es la distancia 2a entre vértices.
• Eje imaginario: es la distancia 2b de los puntos B₁ y B₂. Los puntos B₁ y B₂ se generan como vemos en las relaciones entre semiejes. Así pues, existe una relación entre los semiejes y la distancia focal:
  
  
  
  
• Asíntotas: son las líneas rectas (A₁ y A₂) que se aproximan a la hipérbola en el infinito.
• Puntos interiores y exteriores: la hipérbola divide el plano en tres regiones. Dos regiones que contienen un foco cada una y otra región sin ningún foco. Los puntos contenidos en las regiones con un foco se llaman interiores (I) y los otros exteriores (Ex).
• Tangentes de la hipérbola: sobre cada punto P_i de ambas ramas de la misma. Cada tangente es la bisectriz de los dos radios vectores del punto P_i.

• Circunferencia principal (CP): su radio r=a y su centro en O. Es el lugar geométrico de las proyecciones de un foco sobre las tangentes.
• Directrices de la hipérbola: son dos rectas paralelas al eje transverso (D₁ y D₂). Su distancia a cada una es a/e (e es la excentricidad de la hipérbola). Pasan por las intersecciones de la circunferencia principal con las asíntotas (A₁ y A₂).

Hipérbola equilátera

La hipérbola equilátera es la que tiene sus asíntotas (A₁ y A₂) perpendiculares entre sí, o, dicho de otra manera, cuando forman un ángulo con cada eje de 45º.

Relación entre semiejes de la hipérbola

Las semiejes de la hipérbola (a y b) se relacionan con la distancia focal (c) por la siguiente fórmula:



Geométricamente podemos encontrar los puntos B₁ y B₂. Para ello, se trazan las rectas tangentes a la hipérbola en los vértices V₁ y V₂. Las dos tangentes cortarán en las asíntotas en cuatro puntos. Unimos los segmentos dos a dos siendo de longitud 2a y perpendicular al eje no transverso. Los dos puntos producto de la intersección de los dos segmentos y el eje no transverso serán B₁ y B₂. Siendo O=(o₁,o₂) el centro de la hipérbola, tendremos que B₁=(o₁,o₂+b) y B₂=(o₁,o₂-b).
De esta forma, se podría calcular el semieje imaginario (b) a partir del semieje real (a) y la semidistancia focal (c):

Ecuación de la hipérbola

La ecuación de la hipérbola se puede expresar cuando su centro es O=(o₁,o₂) como:



Si la hipérbola tiene su centro en el origen, O=(0,0), su ecuación es:



Además, los puntos de una hipérbola son los que cumplen la ecuación general de la hipérbola:



siendo A, B, C, D y E escalares (números reales) y necesariamente debe cumplir que los coeficientes de x² e y² (A y C) son no nulos y tienen diferente signo.

Asíntotas de la hipérbola

Las asíntotas de la hipérbola (A₁ y A₂) son las dos líneas rectas que se aproximan cada vez más a la hipérbola pero no llegan a intersectarla. En el infinito las asíntotas estarán a una distancia 0 de ella.
Las ecuaciones de las asíntotas se pueden obtener si se conocen el semieje real (a) y el semieje imaginario (b).

Excentricidad de la hipérbola

La excentricidad mide lo “abierta” que es la hipérbola. Puesto que c (semidistancia focal) es siempre mayor que a (semieje real), la excentricidad de la hipérbola es siempre mayor que la unidad.



La excentricidad es mayor o igual a 1. Si ésta es muy próxima a 1, la hipérbola tiende a una recta partida. Cuando la excentricidad crece, la hipérbola tiende a dos rectas paralelas al eje no transverso, o dicho de otra forma, las dos ramas de la hipérbola están más abiertas.



La excentricidad también se puede calcular a partir de los semiejes (a y b) mediante la fórmula:

Construcción de la hipérbola por puntos

Veamos una forma sencilla para la construcción geométrica de la hipérbola, conociendo el eje real (V₁V₂=2a) y la distancia focal (F₁F₂=2c).

• Dibujamos la línea del eje focal E, sobre la que marcamos los dos vértices V₁ y V₂ y su centro O, equidistante de ellos una distancia a. Marcamos también los dos focos, equidistantes del centro O una distancia c.
• Ahora, sobre el mismo eje y a partir del segmento 2c hacia afuera, marcamos unos puntos cualquiera, supongamos que cuatro: P₁, P₂, P₃, P₄.
• Con un compás, en cada uno de ellos tomamos dos radios, r=P₁V₁ y r’=P₁V₂.
• Con esos radios y centros en los dos focos F₁ y F₂ trazamos arcos. Los cuatro puntos donde se cortan son puntos de la hipérbola.
• Repetimos el proceso con P₂, P₃ y P₄.
• Si unimos los puntos obtenidos, apoyándonos sobre las asíntotas, obtendremos la hipérbola.
• Vemos que cada uno de esos puntos cumple ri – ri’ = d1 – d2 = 2a, que, como se han trazado con centro en los dos focos, cumple la definición de la hipérbola.